Neural Graph Collaborative Filtering

NOTE: This paper's implementation in TypeScript Programming is published on Github, repo: https://github.com/PrinOrange/ts-ngcf , and paper: https://dl.acm.org/doi/10.1145/3331184.3331267

Key Conceptions

• Collaborative Filtering: It denotes the implicit group-behavior patterns for interactions between users and objects(for example, clicking, voting and purchasing). It's used for speculating user's preferences and correlations among objects. It assumed that behaviorally similar users would have similar preferences on items. CF has two key components, embedding and modeling.
• Interaction modeling: A progress of reconstructing historical interactions based on the embeddings, the interaction function details could be based on factor matrix, non-linear neural networks and Euclidean distance metrics.
• Embedding: Learning vector representations of users and items. For convenience, we vectorize the features from users and items, and transform them into vector form.
• Collaborative signal: The implicit correlations between users and objects. It indicates where are the user's interests in between objects and their behaviors.
• bipartite graph: It's a special graph structure whose nodes can be divided into two non-intersecting sets, and each edge in the graph can only connect nodes in these two sets, while there is no direct connection between nodes in the same set.
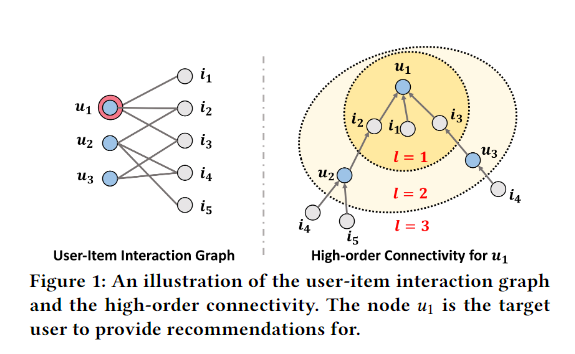
• High-order connectivity: refers to multi-hop interaction paths (such as user A → item 1 → user B → item 2), which can reflect potential interest associations, user A might be interested in item 2
• Decay factor: The decay factor is an important hyperparameter used to control the attenuation of the influence of neighbor nodes on the target node as the number of path hops increases during information propagation. Its core function is to balance the weights of local information and global information and avoid noise interference from high-order neighbors.
• LeakyReLU is an activation function. It is an improved version of ReLU (Rectified Linear Unit) and is used to solve the "dead neurons" problem that may occur during ReLU training.
• element-wise product: In the recommendation system, it is used to represent the relationship between user and item embedding
• BPR Loss: It's a loss function used for description of loss in recommendation to compare the priority between two items.

What problem does this paper solve.

Traditionally the recommendation methodology uses the matrix and deep learning to take user's attributions and item's inherent features into consideration, but it has defects that it ignored the implicitly latent factors(namely collaborative signal) during encoding progress.

For example, there is a pregnant user and she wants to purchase a milk powder, the tradition methodology tags this user with baby, pregnant, infant, while the goods of milk powder are tagged with baby food. Then the recommendation system simply could only capture that tags baby, infant from user and tags baby food from milk powder are in one class, and recommend milk powder list to user. The system matches these tags directly (baby <-> baby food) and recommends milk powder because the tags are explicit factor.

But it ignored that a pregnant user not only needs the milk powder simply but also other relevant goods, she may be need milk bottle and nipple after she brought the milk powder for her baby.

So there is the implicitly latent correlation between "purchasing milk powder" and "milk bottle", "nipple". That is namely collaborative signal.

The traditional methodology has such defect and that is what's the paper focusing on. This paper prompt a new idea that integrates user-item interactions as collaborative signal into embedding process with structure named bipartite graph , and it develop a new framework named Neural Graph Collaborative Filtering which could exploits these latent factors and establish high-order connectivities between users and items with such data structure, and effectively inject the collaborative signals into embedding process.

The authors occurs that some methods for interaction modeling, like MF, nonlinear neural network, are not enough for embedding for they lacks the encoding for collaborative signals that could not take advantages of implicit interest correlations from behaviors.

Also, the authors devised many benchmark tests over this framework and verified its rationalities and improvements.

How to embark on

The difficulty authors faced on is that information system may have large-scale dataset so that its hard to distill and refine the collaborative signal. So the authors deal with this problem by exploiting high-order connections from user-item reactions with encoding collaborative signal into reaction graph.

The authors are inspired by recent works of graph neural networks, and compared existing HOP-Rec to NGCF, pointed out that HOP-Rec still be based on MF thar can not enough exploit training data. NGCF incorporates high-order connectivity directly into the model architecture and dynamically adjust the embedding representation through embedding propagation to generate better embeddings.

The figure 1 indicates how and what information does this graph provides. There are lines connect $(u_{1})$ to $(i_{1})$, $(i_{2})$ and $(i_{3})$ and it means there are semantically behavioral relationships between user $(u_{1})$ with $(i_{1})$, $(i_{2})$ and $(i_{3})$

Recommendation process for user $(u_{1})$:

• First-level propagation: $(u_{1} \leftrightarrow i_{2})$ (direct interaction).
• Second-level propagation: $(u_{1} \leftrightarrow i_{2} \leftrightarrow u_{2})$ (discovering similar behavior to $(u_{2})$).
• Third-level propagation: $(u_{1} \leftrightarrow i_{2} \leftrightarrow u_{2} \leftrightarrow i_{4})$ (inferring that $(u_{1})$ may like $(i_{4})$)

The model also decides which of $(i_{4})$ and $(i_{5})$ is more suitable to recommend to $(u_{1})$ through the learned information flow weights. Obviously, the count of paths connected $(u_{1})$ to $(i_{4})$ are more than $(i_{5})$.

More details, see page 2, Running Example and Present Work section.

Methodology

The methodology of NGCF contains three lines:

• Initialize embedding layer for user and item.
• Multi embedding propagation layers to refine embeddings by injecting high-order connectivity.
• Prediction layer to aggregate refined embeddings and output final affinities score for user-item tuple.

First-order propagation

The users that consume an item can be treated as the item's features and used to measure the collaborative similarity of two items. NGCF designs an interaction-aware message construction mechanism that incorporates personalized user-item affinity (implemented through element-by-element multiplication) into the propagation process of graph neural networks, thereby generating more accurate embedding representations.

Each propagation includes two links: message construction and message aggregation.

Message Construction: for a connected user-item pair $((u,i))$, we define the message from $(i)$ to $(u)$ as:

$(m_{u←i} = f(e_{i} ,e_{u} ,p_{ui}),)$

where $(m_{u←i})$ is the message embedding. $(f)$ is the message encoding function, which takes embeddings $(e_{i})$ and $(e_{u})$ as input, and uses the coefficient $(p_{ui})$ to control the decay factor on each propagation on edge $((u,i))$.

How do the authors implement $(f)$, see the normalized formula $((3))$

This message is the unit of propagation in the graph neural network.

Message Aggregation Aggregate $(u)$'s propagations from neighborhoods and refine $(u)$'s representation, denoted with $(e^{(1)}_{u})$, its definition, see formula $((4))$, analogously, we also could denote item's representation by $(e^{(1)}_{i})$

High-order propagation

After first-order propagation we also could stack more propagation layers to explore high-order connectivities and exploit more collaborative signals.

The $(l)$-th order propagation for user representation was denoted by symbol $(e^{(l)}_{u})$, analogously, $(e^{(l)}_{i})$ for $(l)$-th propagation for item. See formula $((5))$.

Also we could define the $(l)$-th propagation message as $(m^{(l)}_{u\leftarrow i})$ and $(m^{(l)}_{u\leftarrow u})$. See formula $((6))$.

Formula $((5))$ and $((6))$ are also could be transcript into formula $((7))$, in matrix form.

Model Prediction

After we solve $(l)$-th layers and propagations we could get final representations for user and item, denoted by $(\{ e^{(0)}_{u}, ..., e^{(l)}_{u} \})$ and $(\{ e^{(0)}_{i}, ..., e^{(l)}_{i} \})$, and concat them respectively. The parameter $(l)$ is used for controlling the layers count and determine how spread the recommendation does.

Finally we conduct the preferences between user and item with such formula towards target item.

And the caculation result is a scalar, indicates the user's preference to specified item in numberic score form. So as we can ranking items according to score number.

Optimization

The author thought that BPR loss used in personalized recommendation systems has rooms for improvement, which aims to optimize the ranking of items through pairwise comparison. Its core idea is that for a certain user, the observed interaction items (such as clicks, purchases) should get higher prediction scores than the unobserved items. And it defined the loss function at formula $((11))$

By the way the author compared NGCF to MF based recommendation system, NGCF has two extra optimized advantages,

• Lower model size: It only depends on embedding look-up matrix $(E^{(0)})$that transformed from user-item graph and weight matrix, with only $(2Ld_{l}d_{l-1})$parameters, is negligible compared to MD based model.
• Node and message dropout: The authors refer the node and message dropout in traning stage that randomly reduce outgoing message to avoid overfitting.

Model Degradation

In discussion, the author pointed out that NGCF virtually is a expansion of traditional recommendation model SVD++ and NGCF. Including traditional models such as SVD++ and FISM in the same system showed that they were special cases of NGCF. SVD++ and FISM only utilize first-order interactions, while NGCF captures high-order cooperation signals through multi layers propagation, so it has stronger expressive power. Namely, NGCF is a general framework that can cover traditional models such as SVD++ and FISM by adjusting the number of propagation layers, message weights, and transformation functions.

Downgrade to FISM: in formula NGCF-SVD , set $(p_{iu'} = 0)$, namely prevent connection between user and items, NGCF has same behavior with FISM.

Downgrade to SVD++: if higher-order propagation is prohibited, multiple layers are not stacked, and only direct neighbor with first-order interaction information is retained, then NGCF would be downgraded to SVD++.

Time Complexity

This model involved matrix multiplication, for $(l)$-th propagation, it needs triple-order matrix multiplication, with sizes of $(|R^{+}|)$, $(d_{l})$, $(d_{l-1})$

Also in $(l)$-th traning stage is $(|R^{+}|d_{l})$.

The summary of time optimization for whole procession is

MF & Graph based model

It discusses two major problems of modern recommender systems:

1. Traditional methods such as matrix decomposition uses inner products to model user-item interactions, but their linear capabilities are limited;

2. Deep learning methods: such as NeuMF use neural networks to capture nonlinear interactions, but still implicitly learn collaborative filtering signals and cannot guarantee behavioral transitivity (such as indirectly related users/items are close in embeddings).

current models lack explicit encoding process of collaborative filtering signals (such as transitivity), resulting in poor embedding quality.

Briefly speaking, a better recommendation systems relied on implicit learning of user-item relationships, and need to explicitly model behavioral transitivity to improve embedding effects.

Recent years, research on recommendation system based on user-item interaction graphs has made some progress. early methods such as ItemRank and BiRank used label propagation technology to infer user preferences through node similarity in the graph structure.

These methods are essentially neighborhood-based recommendations, but due to the lack of optimizable model parameters, their performance is often inferior to that of embedding-based models, to overcome this limitation, new methods such as HOP-Rec combine high-order connectivity information obtained by random walks with matrix decomposition and train recommendation models through the BPR objective function. It have shown that this method combined with graph structure can effectively improve the recommendation effect. However, existing methods still have obviously shortcomings: on the one hand, high-order connectivity is only used for data enhancement and is not directly integrated into the embedding function, on the other hand, the effect of random walks is highly dependent on the tuning of hyperparameters such as the attenuation factor, which makes the stability of the model challenging. Overall, current research has not fully explored the potential of graph structure information.

How to directly encode high-order relationships into the embedding learning process is still a key issue that needs to be solved.

Experiments

Authors perform experiments on three real-world datasets to evaluate our proposed method, especially the embedding propagation layer. And they aim to answer the following research questions:

• How does NGCF perform as compared with latest CF methods?
• How do different hyper-parameter settings, like depth of layer, embedding propagation layer, layer-aggregation mechanism, message dropout, and node dropout affect NGCF?
• How do the representations benefit from the high-order connectivity?