A Star Algorithm
A* search algorithm is a path finding algorithm that finds the single-pair shortest path between the start node(source) and the target node(destination) of a weighted graph.
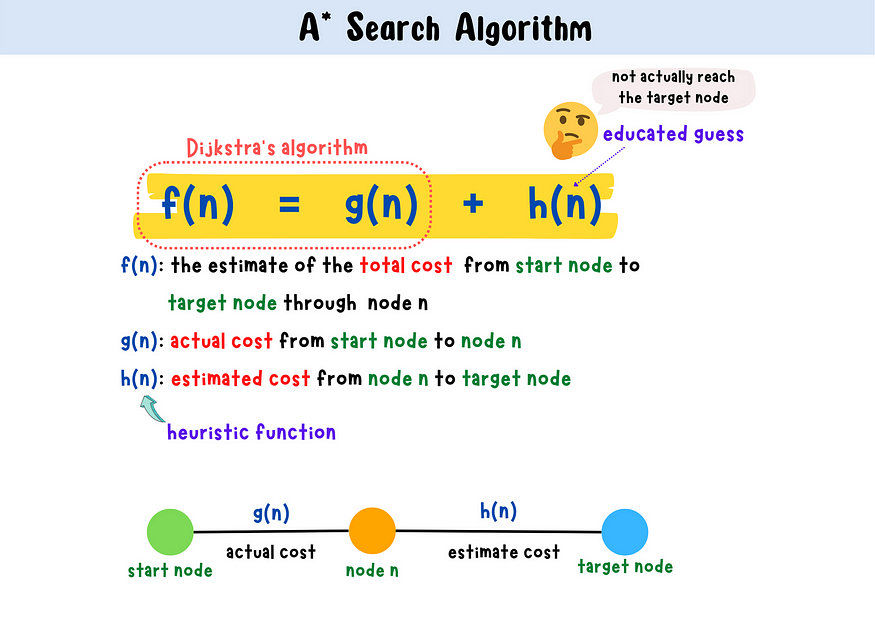
Asearch algorithm is a path finding algorithm that finds the single-pair shortest path between the start node(source) and the target node(destination) of a weighted graph. The algorithm not only considers the actual cost from the start node to the current node(g) but also tries to estimate the cost will take from the current node to the target node using heuristics (h). Then it selects the node that has the lowest f-value(f=g+h) to be the next node to move until it hits the target node. Dijkstra's algorithm is a special case of A algorithm where heuristic is 0 for all nodes.
How A* Algorithm Works?
The formula for A* algorithm considers two functions, g(n) and h(n). Imagine that we are currently at node n, g(n) tells us the actual cost we took from the start node to the current node. h(n) is a heuristic function that estimates the cost we will take to get to the target node from the current node. Therefore, h(n) is an educated guess and it is crucial to determine the performance of A* algorithm. Based on the sum of the g(n) and h(n), f(n), the algorithm is able to estimate the total cost from the start node to the end node.
f(n) = g(n) + h(n) , f(n): the estimate of the total cost from start node to target node through node n
g(n): actual cost from start node to node n
h(n): estimated cost from node n to target node
The algorithm selects the minimum f-value node as the next current node to explore and continuously update g(n) and h(n) if a better path is found for nodes it encountered. This process continues until the algorithm reaches the target node.
A* algorithm vs. Dijkstra's algorithm
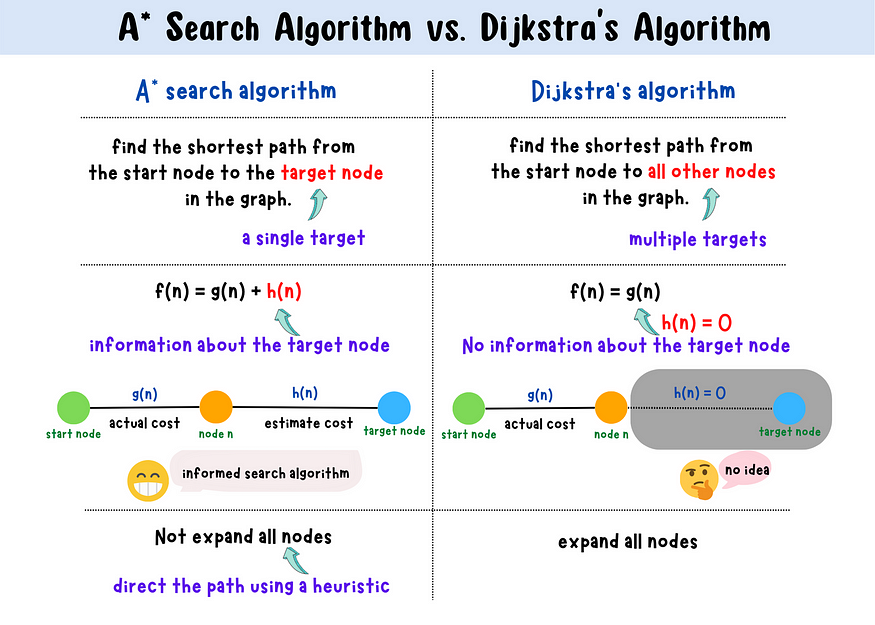
A* Algorithm only finds the shortest path between the start node and the target node, whereas Dijkstra's algorithm finds the shortest path from the start node to all other nodes because every node in a graph is a target node for it.
A* algorithm runs faster than Dijkstra's algorithm because it uses a heuristic to direct in the correct direction towards the target node. However, Dijkstra's algorithm expands evenly in all of the different available directions because it has no knowledge regarding the target node before hand, it always processes the node that is the closest to the start node based on the cost or distance it already took.
Graphical Explanation
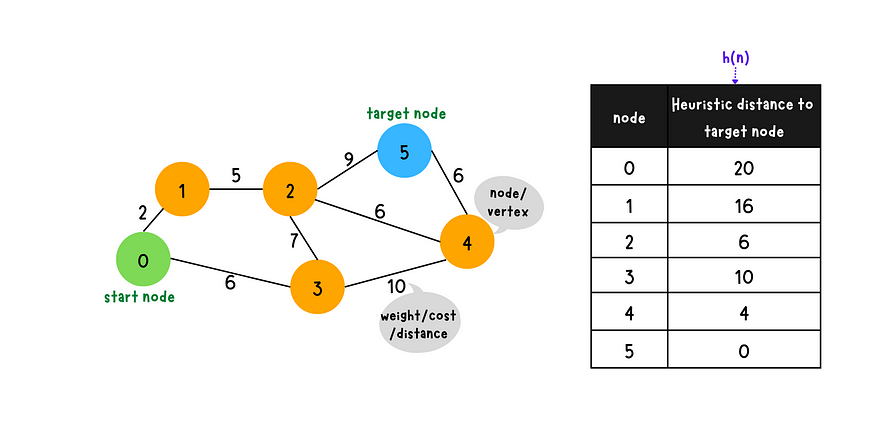
Heuristic is crucial to the performance of A* algorithm. The heuristic function we use here just for the demo purpose.
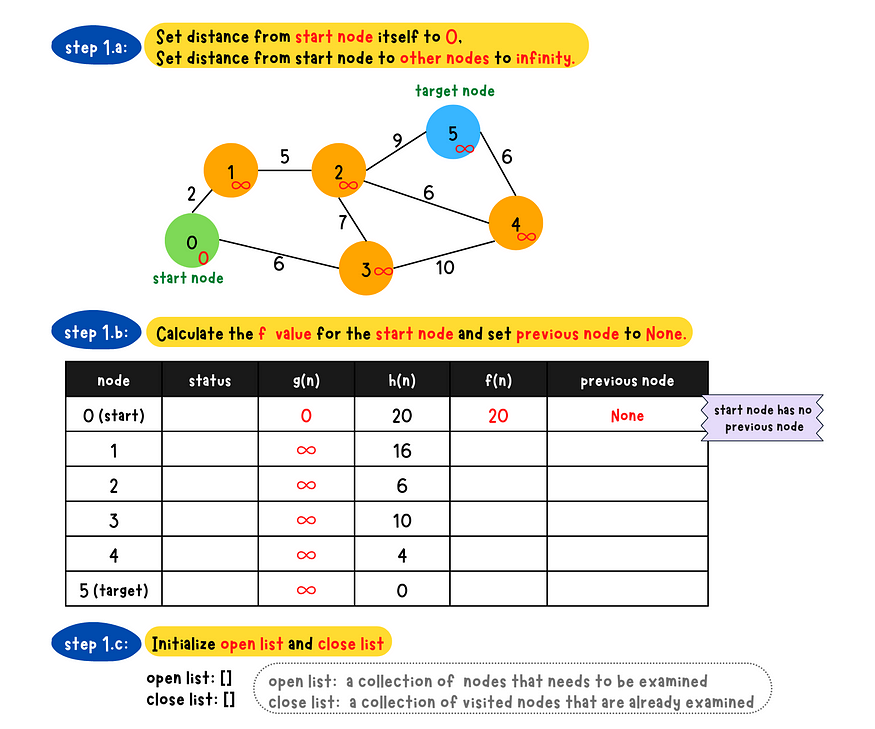
- Step 1
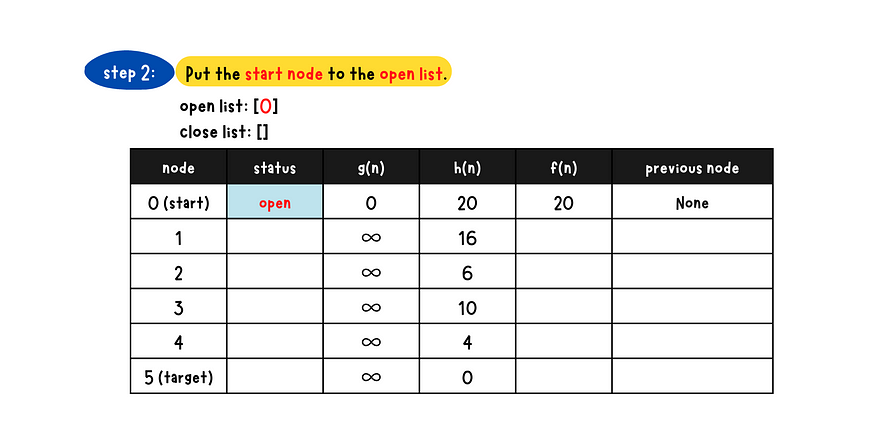
- a: Set the distance to the start node itself to 0 and the distance to all other nodes to infinity.
- b: Calculate the f value for the start node and set the previous node to none/nil/null.
- c: Initialize an open list and close list which are empty initially.
- Step 2: Place the start node into the open list
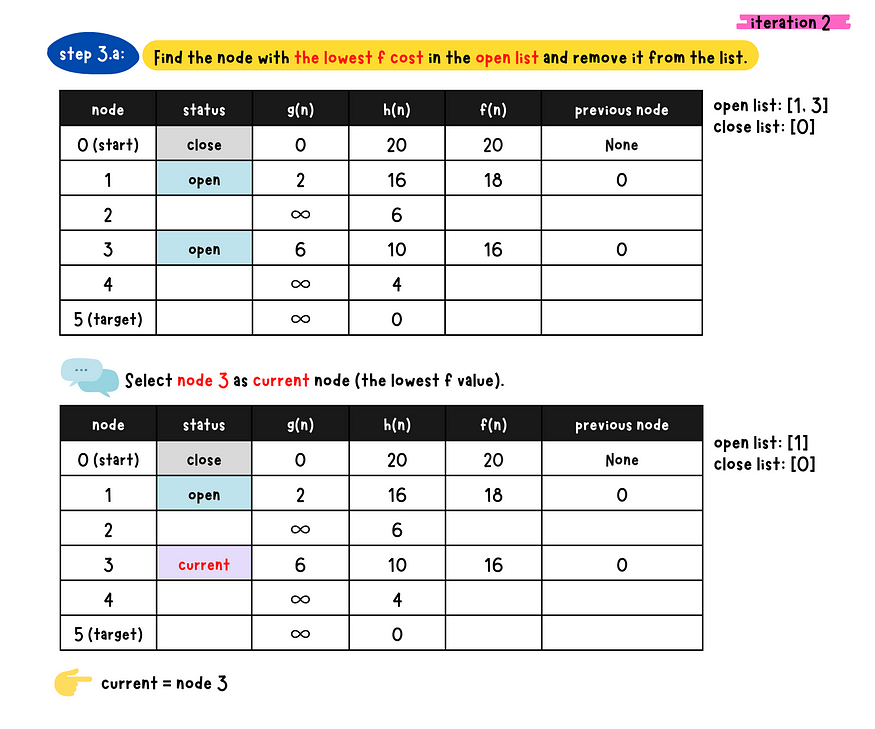
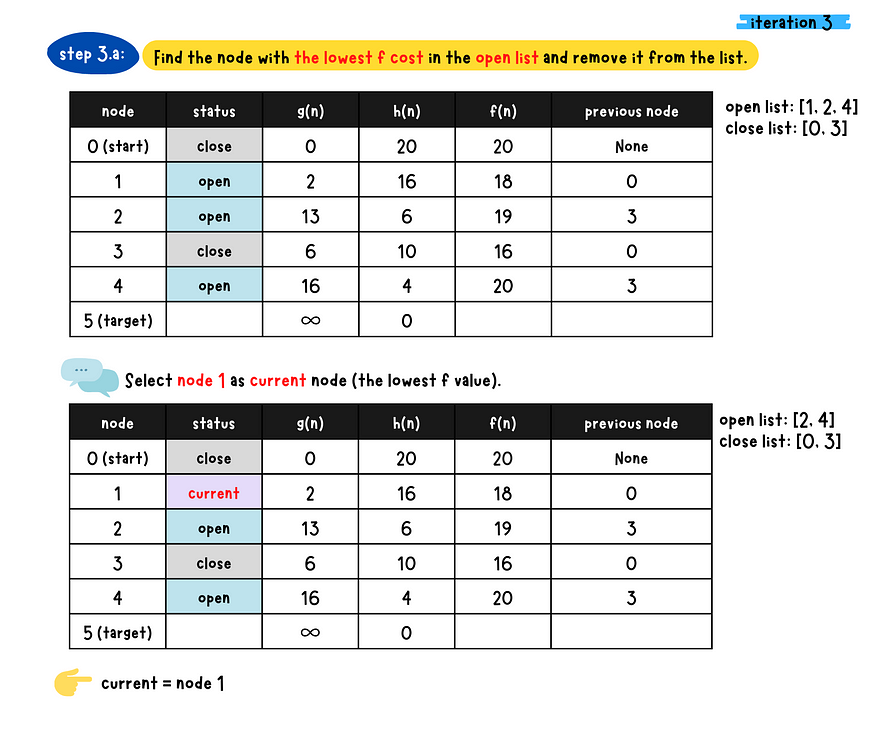
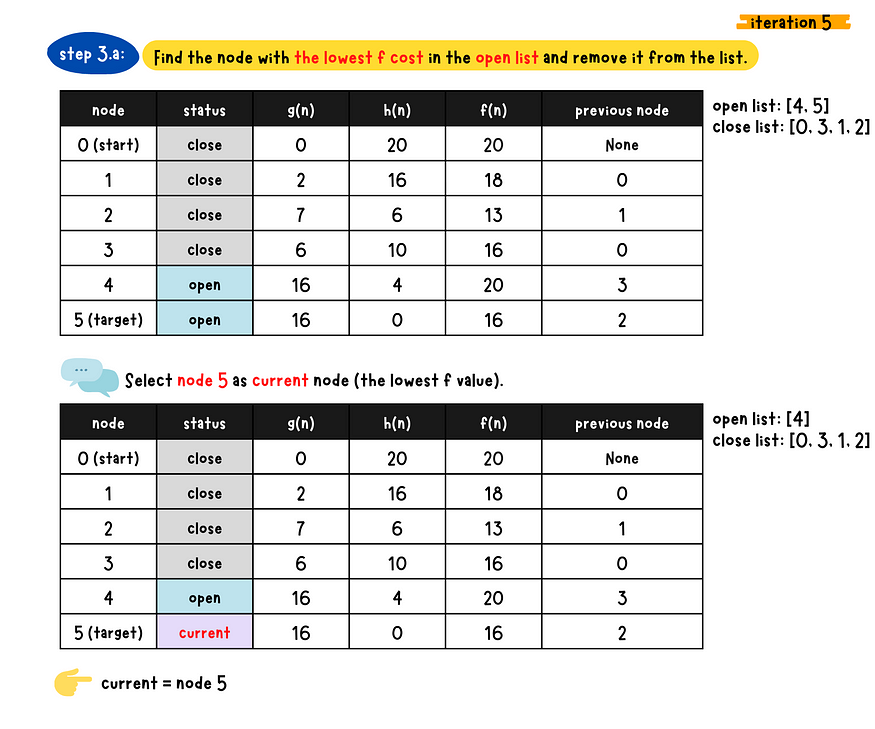
- _Step 3
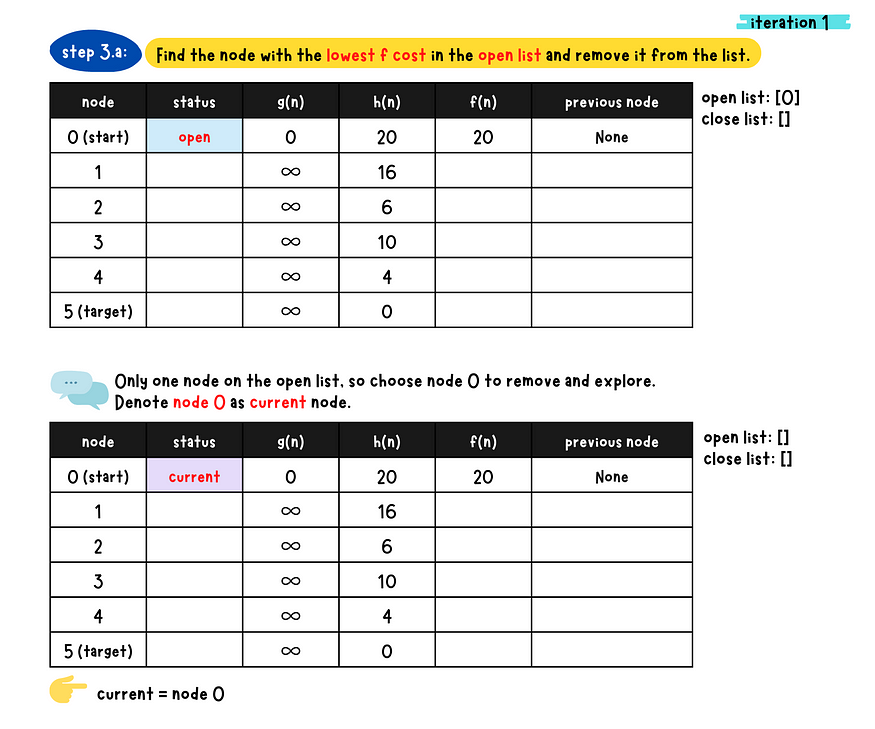
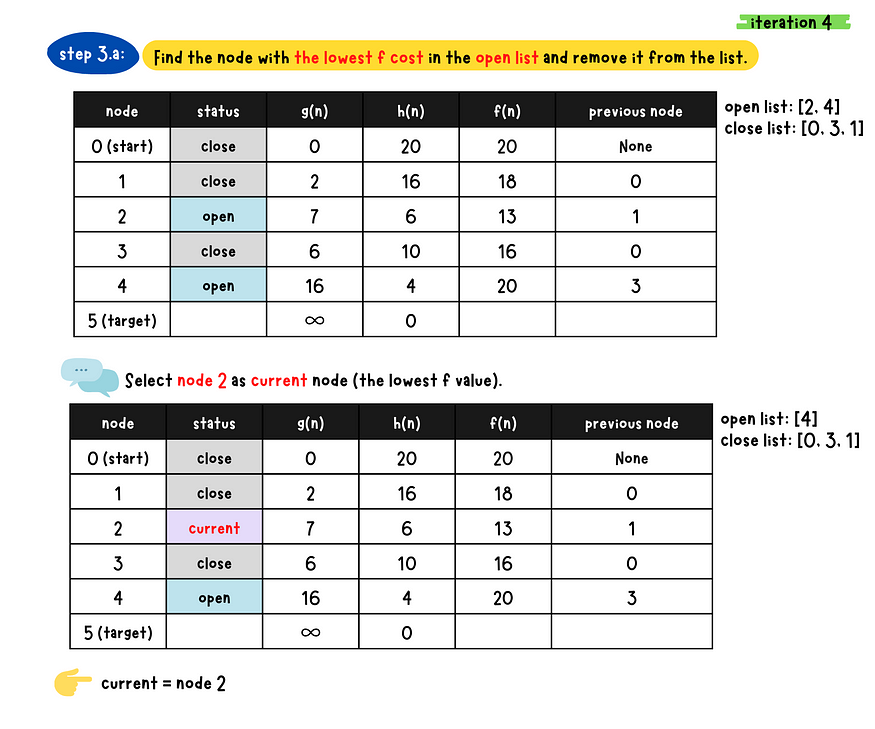
_*-* a*:* Find the node with the minimum f-value in the open list and removed from the list. Denote this node as the current node.
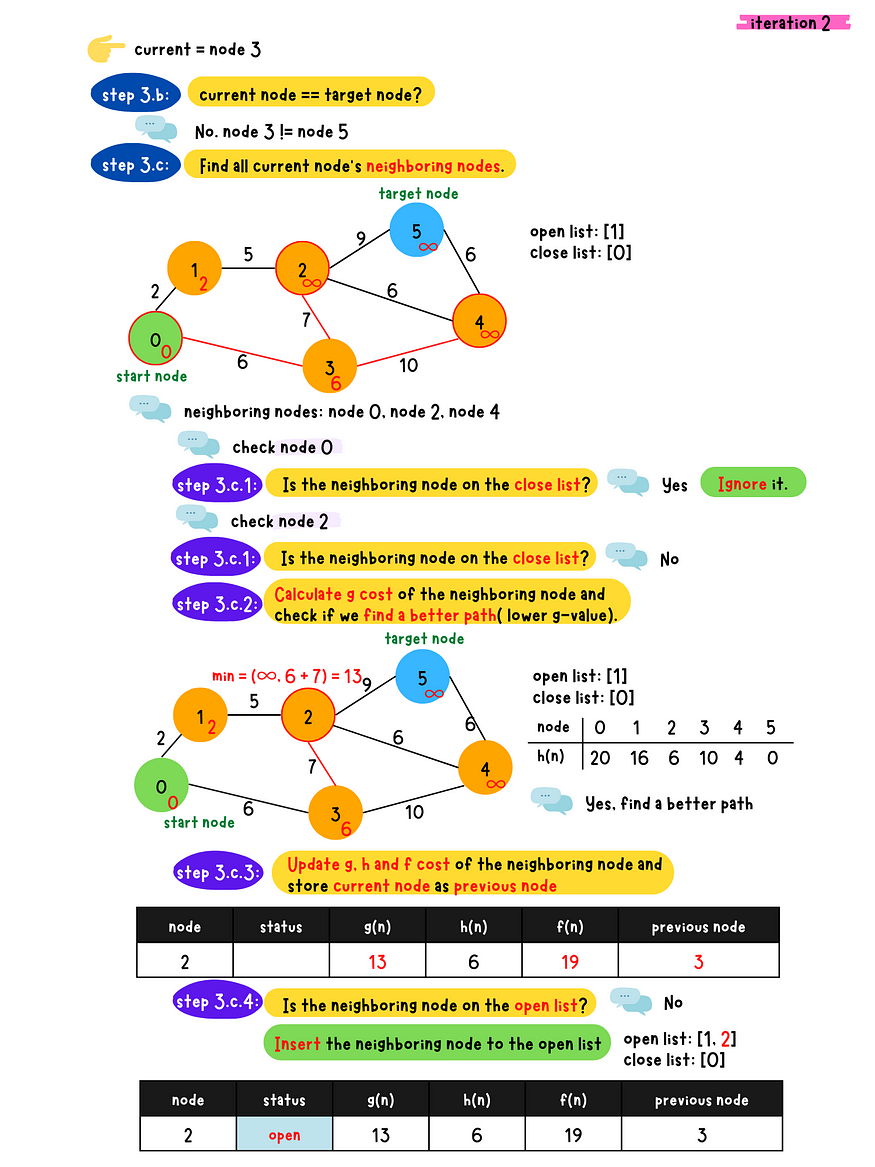
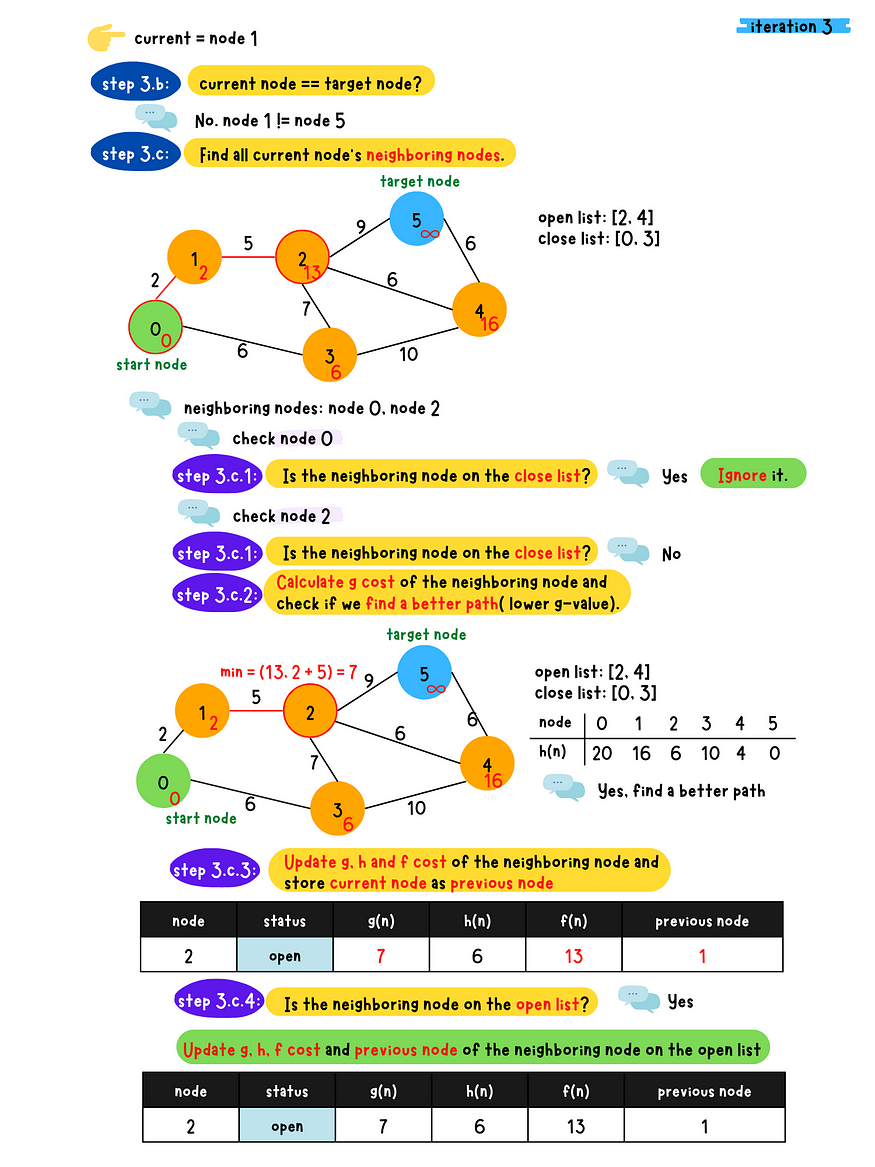
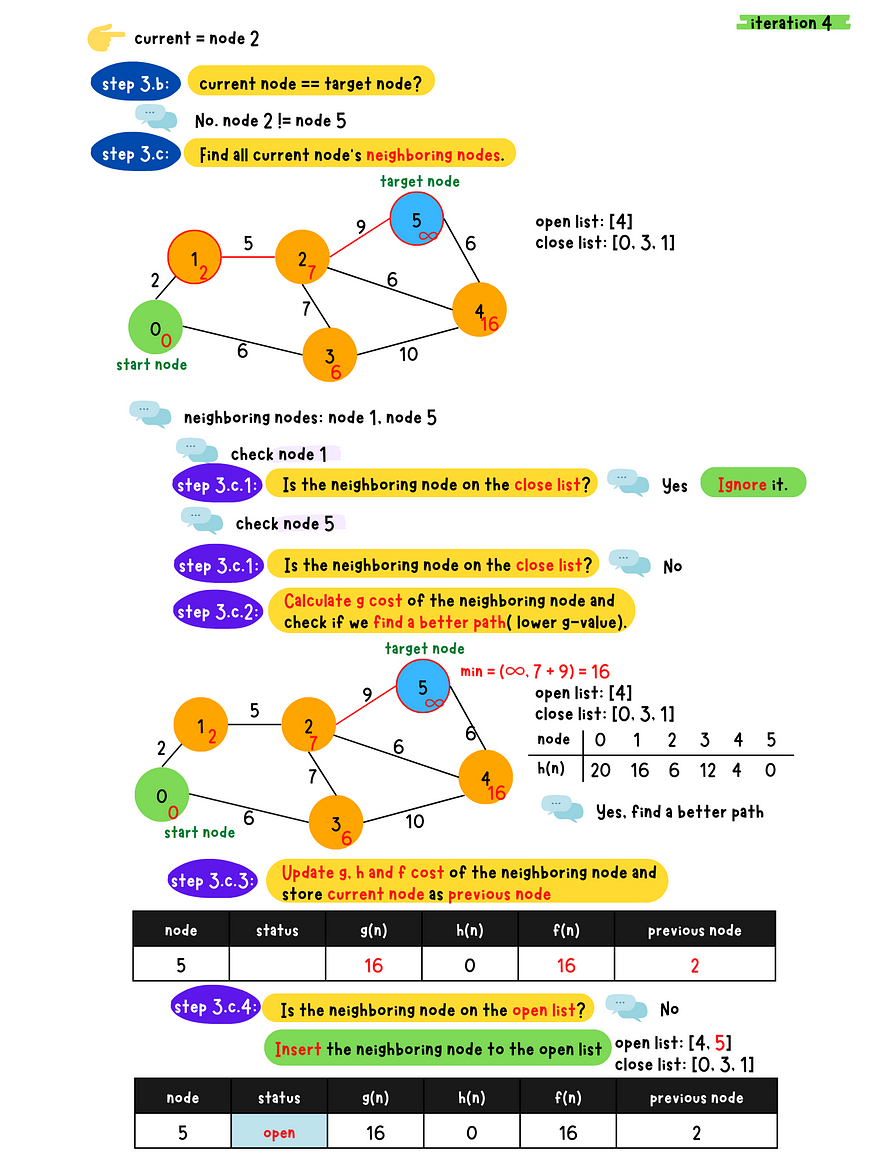
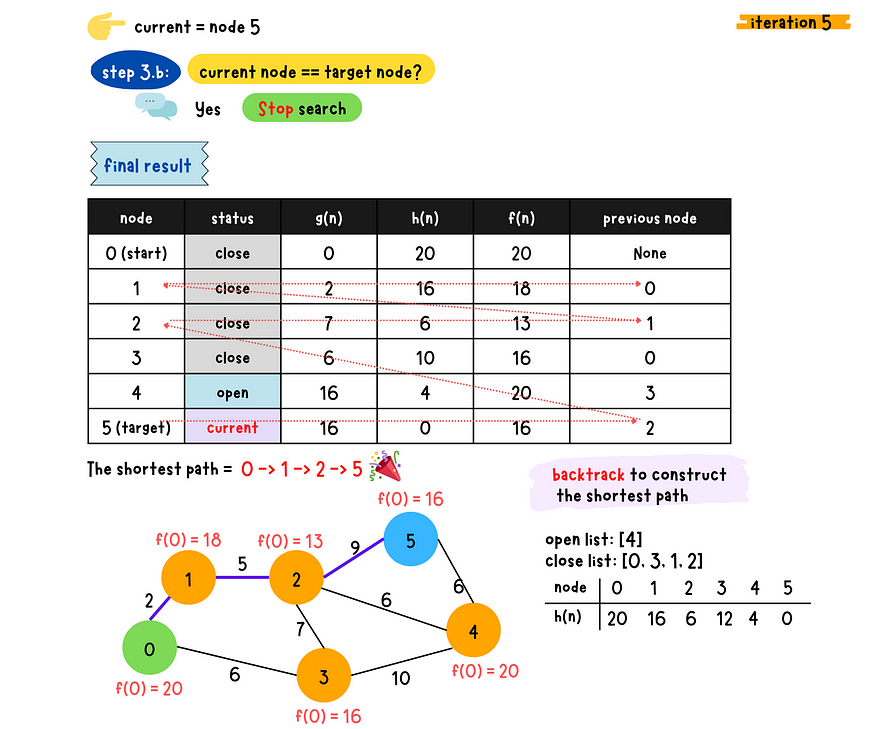
- b: Check if the current node is the target node or not
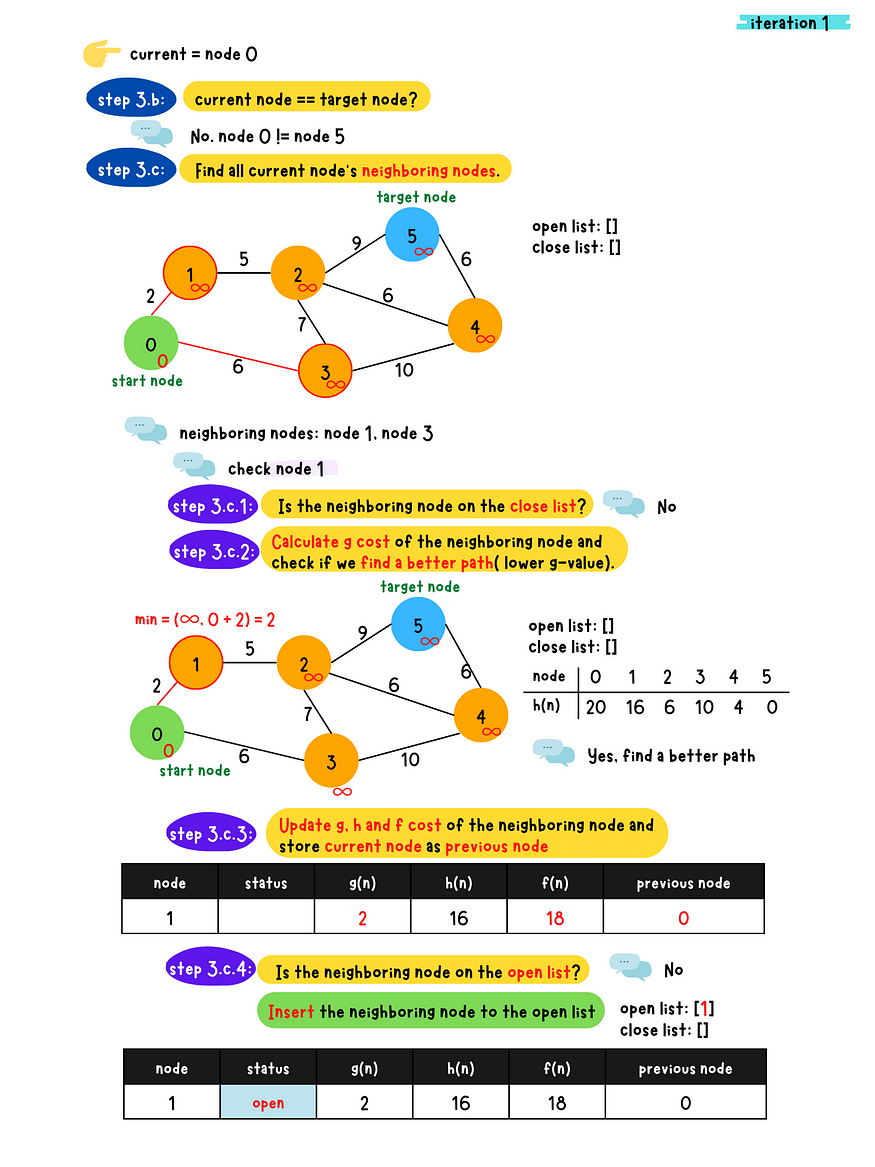
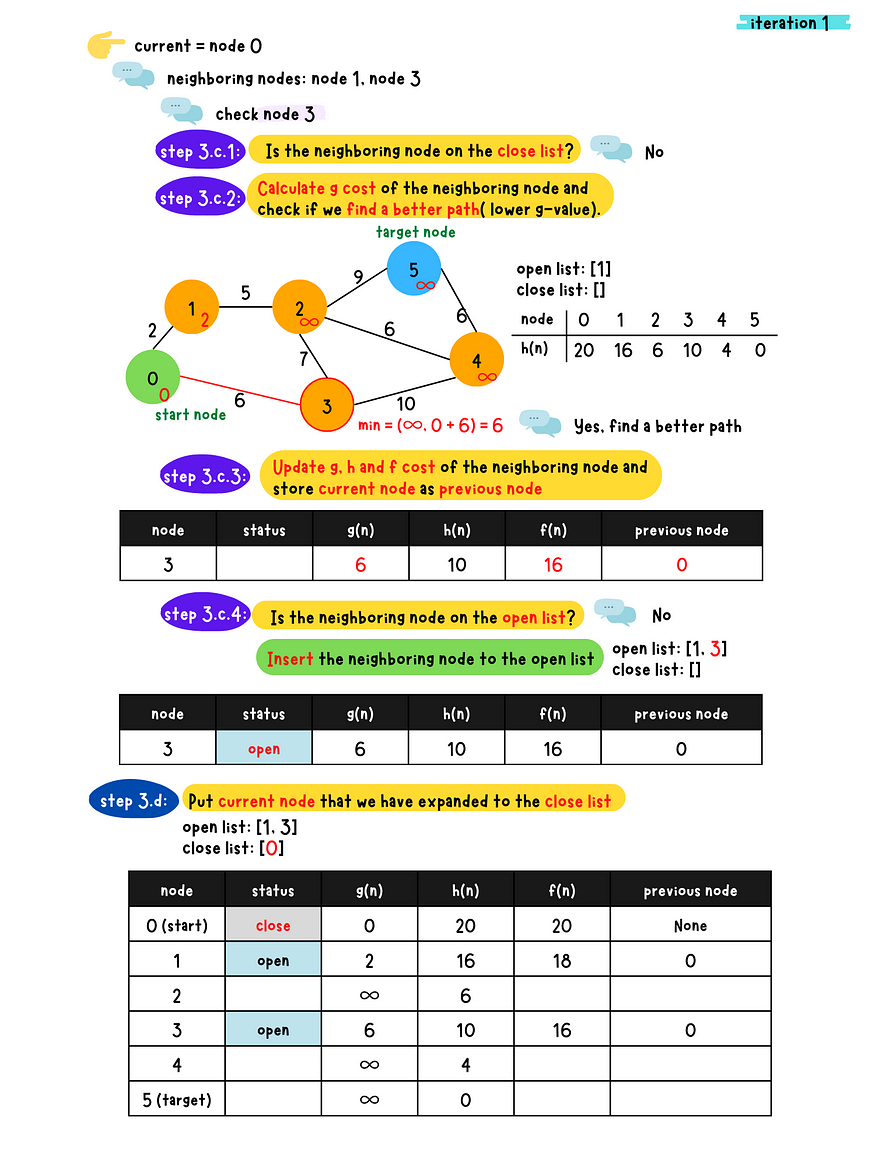
- c: Populate all the current node's neighboring nodes and do following checks for each neighboring nodes
1. Is the neighboring node in the close list?
- Yes. Skip this node.
- No. Go to 2.2. Calculate g value for the neighboring node and check if a better
path(lower g value) is found? - No, Skip this node - Yes. Go to 3.3. Calculate g, h and f value for the neighboring node and set
the previous node to the current node**4. Check if the neighbor node in the open list?** - Yes. Update g, h and f value of the neighboring node in the
open list - No. Insert this neighboring node to the open list
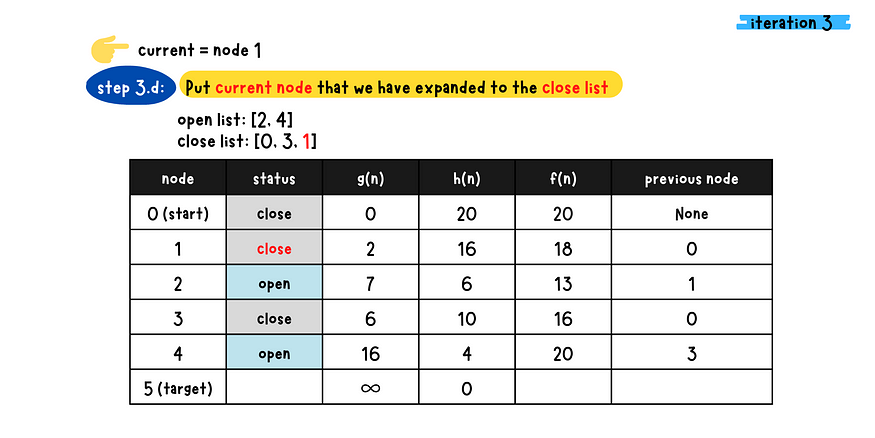
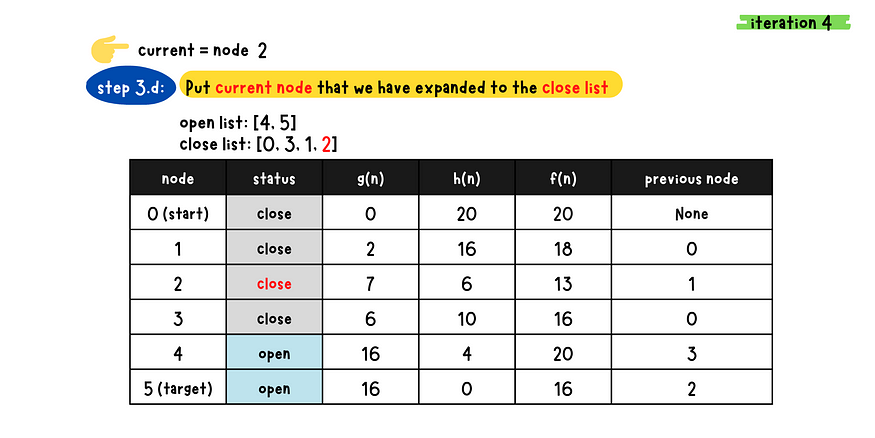
- d: Place the current node to the close list because we have expanded this node.
- Step 4: Repeat Step 3 until reaches the target node
demo iteration 1
demo iteration 2
demo iteration 3
demo iteration 4
demo iteration 5
final result
At the end, we can backtrack the shortest path using the previous node. In this demo, we use A* algorithm to search the shortest path without necessarily search all the graph.(We haven't examined node 4 yet, so you can see the node 4 is till on the open list). Unlike Dijkstra's algorithm, it has to expand all the nodes in the graph.
You can check here to know more about Dijkstra's algorithm.
Code Implementation
Data Structure
Use Priority queue to get the lowest f-value node for each run. In this demo, we implement code using min heap data structure .
Complexity
Time: O(nlog(n)), Space: O(n)
n: the total number of nodes in the graph
Pseudocode
initialize a min Heap contains the start node
minHeap = MinHeap([start])While minHeap is not empty:
grab the minimum f-value node from minHeap and denote as current
current = minHeap.pop() # check if current is the target node
if current == target:
break
populate all current node's neighbors
for neighbor in current.neighbors:
compute neighbor's g, h, f value
if neighbor in minHeap:
if neighbor.g < neighbor.g in minHeap:
update minHeap
else:
insert neighbor into minHeap
Python
- code
from min_heap import MinHeap
class Node:
def __init__(self, nodeId, hValue):
self.id = nodeId # use node idx as id
self.g = float("inf") # distance from the start node to the current node
self.h = hValue # estimate distance from the current node to the target node
self.f = float("inf") # total cost from the start node to the end node
self.previousNode = None # use for backtrack
def AstartAlgorithm(graph, start, target, hValues):
nodes = initializeNodes(graph, hValues)
startNode = nodes[start]
targetNode = nodes[target]
# set distance to start node itself to 0
startNode.g = 0
startNode.f = startNode.g + startNode.h
# init open list and close list
openList = MinHeap([startNode]) # nodes to be expanded
# closeList = set() # nodes have expanded
# repeat until the openList is empty
while not openList.isEmpty():
# remove the node with the lowest f-value
currentNode = openList.remove()
if currentNode == targetNode:
break
# populate all current nodes neighbors
neighbors = graph[currentNode.id]
for neighbor in neighbors:
neighborIdx, distanceToNeighbor = neighbor
neighborNode = nodes[neighborIdx]
# check if neighbor in close list
# if neighborNode in closeList:
# continue
# check if find a better path
newNeighborG = currentNode.g + distanceToNeighbor
if newNeighborG >= neighborNode.g:
continue
# update neighbor's g, h, f and previousNode
neighborNode.previousNode = currentNode
neighborNode.g = newNeighborG
neighborNode.f = neighborNode.g + neighborNode.h
# check if the neighbor in the openList
if not openList.containsNode(neighborNode):
openList.insert(neighborNode)
else:
openList.update(neighborNode)
# put current node to close list
# closeList.add(currentNode)
return backtrackPath(targetNode)
def initializeNodes(graph, hValues):
nodes = []
for i in range(len(graph)):
nodes.append(Node(i, hValues[i]))
return nodes
def backtrackPath(targetNode):
if targetNode.previousNode is None:
return []
currentNode = targetNode
path = []
while currentNode is not None:
path.append(currentNode)
currentNode = currentNode.previousNode
return path[::-1]
if __name__ == "__main__":
hValues = [20, 16, 6, 10, 4, 0]
graph = [
# for vertex 0
[
[1, 2], [3, 6]
],
# for vertex 1
[
[0, 2], [2, 5]
],
# for vertex 2
[
[1, 5], [3, 7], [4, 6], [5, 9]
],
# for vertex 3
[
[0, 6], [2, 7], [4, 10]
],
# for vertex 4
[
[2, 6], [3, 10], [5, 6]
],
# for vertex 5
[
[2, 9], [4, 6]
],
]
# startNode = 1, targetNode = 5
path = AstartAlgorithm(graph, 0, 5, hValues)
print("The shortest path")
print("order, nodeId, f-value")
for idx, node in enumerate(path):
print(idx+1, node.id, node.f)
"""
The shortest path
order, nodeId, f-value
(1, 0, 20)
(2, 1, 18)
(3, 2, 13)
(4, 5, 16)
"""
- min heap
class MinHeap:
def __init__(self, array):
self.nodePositionInHeap = {node.id: idx for idx, node in enumerate(array) }
self.heap = self.buildHeap(array)
# Time: O(n) | Space: O(1)
def buildHeap(self, array):
lastParentNodeIdx = (len(array) - 2) // 2
for currentIdx in range(lastParentNodeIdx, -1, -1):
self.siftDown(currentIdx, len(array)- 1, array)
return array
# Time: O(logn) | Space: O(1)
def remove(self):
if self.isEmpty():
return
self.swap(0, len(self.heap)-1, self.heap)
nodeToRemove = self.heap.pop()
del self.nodePositionInHeap[nodeToRemove.id]
self.siftDown(0, len(self.heap)-1, self.heap)
return nodeToRemove
# Time: O(logn) | Space: O(1)
def insert(self, node):
self.heap.append(node)
self.nodePositionInHeap[node.id]= len(self.heap)-1
self.siftUp(len(self.heap)-1, self.heap)
# Time: O(logn) | Space: O(1)
def siftDown(self, currentIdx, endIdx, heap):
childOneIdx = currentIdx*2 + 1
while childOneIdx <= endIdx:
childTwoIdx = currentIdx*2 + 1 if currentIdx*2 + 1 <= endIdx else -1
idxToSwap = childOneIdx
if childTwoIdx != -1 and heap[childTwoIdx].f < heap[childOneIdx].f:
idxToSwap = childTwoIdx
if heap[idxToSwap].f < heap[currentIdx].f:
self.swap(idxToSwap, currentIdx, heap)
currentIdx = idxToSwap
childOneIdx = currentIdx*2 + 1
else:
return
# Time: O(logn) | Space: O(1)
def siftUp(self, currentIdx, heap):
parentIdx = (currentIdx - 1) // 2
while currentIdx > 0 and heap[currentIdx].f < heap[parentIdx].f:
self.swap(currentIdx, parentIdx, heap)
currentIdx = parentIdx
parentIdx = (currentIdx - 1) // 2
def containsNode(self, node):
return node.id in self.nodePositionInHeap
def update(self, node):
# update is occured when a slower f is found
self.siftUp(self.nodePositionInHeap[node.id], self.heap)
def isEmpty(self):
return len(self.heap) == 0
def swap(self, i, j, heap):
self.nodePositionInHeap[heap[i].id] = j
self.nodePositionInHeap[heap[j].id] = i
heap[i], heap[j] = heap[j], heap[i]