Socrates: The Story of Searching for the Largest Ear of Wheat

Sep 21, 2024

This article proposes the classic 37% rule in game theory and its mathematical derivation process.

The Largest Ear of Wheat

It is said that Socrates once led his students for a walk in a wheat field. His students asked him: how can one find the most suitable life partner?

Socrates looked at the wheat field and gave them a task: "Go into the wheat field and find the largest ear of wheat, but as you walk, you can only move forward and cannot turn back."

The students began walking while choosing, and the field was full of large ears of wheat. But which one was the largest? They walked with their heads down, checking one ear of wheat after another. They shook their heads at this one; they shook their heads at that one. They always believed that the largest ear was still ahead. Although they picked a few, they were not satisfied and threw them away. They thought there were plenty of chances and no need to decide too early.

The students continued walking with their heads down, carefully selecting as they went, for quite a long time. Suddenly, they heard Socrates' deep, resounding voice: "You have reached the end." At that moment, the students, empty-handed, realized what had happened and felt disheartened.

Socrates said to them: "There is certainly a largest ear of wheat in this field, but you may not encounter it; and even if you do, you may not make the correct judgment. Therefore, the largest ear is the one you just picked."

This story tells us that life is like walking in a wheat field, also searching for the largest ear of wheat. Some people, upon seeing a full and ripe ear, seize the opportunity and pick it without hesitation; others keep looking around and miss their chances again and again. Of course, the goal should be the largest ear, but holding the one in hand is the most tangible reality.

So, the question arises: Is there a method that can help us find the largest ear of wheat as efficiently as possible?

Treasure Box Game

Let’s consider another example. Imagine there is a gambling game with the following rules: There are $m$ treasure boxes, each containing a random prize amount between $0$ and $x$ dollars, uniformly distributed. However, you don’t know what the maximum amount $x$ in the boxes is. Once you open a treasure box and see the prize, you have two choices: either take the prize and stop, or discard the box and open another one. However, once discarded, a box cannot be chosen again.

Now the question arises: how should you strategize to get the most money possible? Naturally, the more money, the better.

What would happen if we didn’t use any strategy and randomly picked a treasure box?

Let’s assume the amounts in the treasure boxes range from $1000, 999, 998, ..., 0$ , with the top prize being $1000$ . What is the probability of drawing the top prize?

Since each specific amount (including the top prize of $1000) has an equal chance of appearing, and the prize is uniformly distributed, the probability of drawing the top prize can be calculated as follows:

P_{Jackpot} = \frac{1}{(\text{MaxMoney} - \text{MinMoney} + 1)}

In this case, the maximum prize is $1000$ and the minimum is $0$ , so:

P_{Jackpot} = \frac{1}{(1000 - 0 + 1)} = \frac{1}{1001}

Therefore, the probability of randomly picking a treasure box containing the top prize of $1000$ is $0.0999\% ≈ 0.1\%$ . The odds are very low indeed.

Since chasing the jackpot is unrealistic, let’s lower our expectations a bit. What if we aim for a prize of at least $800$ ? What is the probability of winning that?

We can use the formula for uniform distribution. For a prize uniformly distributed between $0$ and $1000$ , the probability density function is constant. The formula for probability is:

P(a \leq X \leq b) = \frac{b - a}{\text{range}}

In this case, the range is from $0$ to $1000$ , so the total range is $1000$ . We want to calculate the probability for the interval from $800$ to $1000$ , so:

P(800 \leq X \leq 1000) = \frac{1000 - 800}{1000} = \frac{200}{1000} = 0.2

Thus, the probability of randomly selecting a treasure box with a prize between $800$ and $1000$ is $20\%$ .

While the probability has increased significantly, $20\%$ is still relatively low.

So, if you randomly pick a treasure box and decide to keep it, the chances of getting a high prize are still slim, which clearly isn’t the optimal strategy.

Optimization

In most cases, we don’t know the maximum prize inside the treasure boxes. Just like in the story of Socrates' students picking the largest ear of wheat, they didn’t know how big the largest ear was.

Let’s change our approach. Even though we don’t know the maximum prize, we do know that if we sample a portion of the treasure boxes, the probability of finding the jackpot in the sample is equal to its probability in the entire set. By sampling some treasure boxes, we can estimate the value of the jackpot based on the maximum prize in the sample.

Let’s denote the jackpot in the entire set as $M$ . Since the jackpot is uniformly distributed among the treasure boxes, we can take a sample from the boxes and record the maximum prize in that sample, denoted as $M'$ . Clearly, this sample maximum $M'$ will be close to the overall jackpot $M$ .

Sampling a portion of the boxes to estimate the jackpot $M$ is feasible, and the more samples we take, the closer $M'$ will be to $M$ .

However, the sample size cannot be too small, or the difference between $M'$ and $M$ will be large, making the estimate ineffective. On the other hand, the sample size cannot be too large either, because there will be fewer treasure boxes left to choose from, reducing the chance of finding the jackpot. Consider an extreme example: if we sample $999$ treasure boxes out of $1000$ , $M'$ will likely be almost equal to $M$ , but with only one treasure box remaining, the chance of hitting the jackpot becomes negligible.

Thus, it is important to balance the sample size with the total number of treasure boxes. Is there an optimal sample size where $M'$ is close to $M$ and the probability of winning a high prize is maximized afterward?

Next, we will use mathematical methods to derive this “balance point.” Suppose the total number of treasure boxes is $m$ , and the sample size is $r$ . We will find the expression for the optimal $r$ .

Mathematical Derivation

Assume we have a total of $N$ treasure boxes, and we select the first $r$ boxes as a sample. In this scenario, we aim to find the optimal sample size $r$ that maximizes the probability of selecting the highest prize after discarding the sample.

Probability Derivation

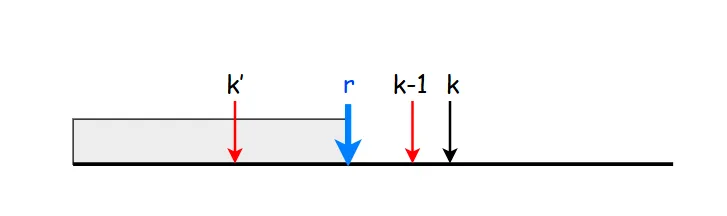
For a fixed $r$ , suppose the highest prize appears in the $k$ -th treasure box. To win the highest prize after discarding the sample, it is necessary that the second-highest prize appears in the first $k-1$ boxes, and specifically, this second-highest prize must also appear within the sample (the first $r$ boxes). The probability of this happening is $\frac{r}{k-1}$ .

This can be visualized with a diagram, where the red arrow indicates the positions where the second-highest prize occurs:

Thus, we derive the following equation:

P = \frac{1}{N} \sum_{k=r+1}^{N} \frac{r}{k-1} = \frac{r}{N} \sum_{k=r+1}^{N} \frac{1}{k-1}

In this equation, $\frac{1}{N}$ represents the probability of the highest prize appearing in the $k$ -th treasure box, and $\frac{r}{k-1}$ represents the probability that the second-highest prize is within the sample of the first $r$ boxes. $P$ is the probability of winning the highest prize after discarding the sample.

Summation Approximation

The above equation contains a harmonic series, which does not have a simple closed form but can be approximated using the following formula:

\sum_{k=1}^{N} \frac{1}{k} = \ln(N) + \gamma

where $\ln(N)$ is the natural logarithm and $\gamma$ is Euler's constant. Here, we want to approximate the summation from $r+1$ to $N$ . To do this, we rewrite the sum as:

\sum_{k=r+1}^{N} \frac{1}{k-1} = \sum_{k=1}^{N-(r+1)+1} \frac{1}{k} = \sum_{k=1}^{N-r} \frac{1}{k}

Thus, the sum starts from $k=1$ and follows the same harmonic series approximation:

\sum_{k=r+1}^{N} \frac{1}{k-1} = \left( \ln(N) + \gamma \right) - \left( \ln(r) + \gamma \right) = \ln(N) - \ln(r)

Finally, using logarithmic properties, we simplify this to:

\ln(N) - \ln(r) = \ln\left(\frac{N}{r}\right)

Substituting into the Original Equation

Now, we substitute the simplified sum into the original probability equation:

P = \frac{r}{N} \ln\left(\frac{N}{r}\right)

Next, we introduce a new variable $x = \frac{r}{N}$ to represent the proportion of the total boxes chosen as the sample, yielding:

P = x \ln\left(\frac{1}{x}\right)

Maximizing the Probability

To maximize $P$ , we take the derivative of $P = x \ln\left(\frac{1}{x}\right)$ with respect to $x$ :

\frac{dP}{dx} = \frac{d}{dx} \left(x \ln\left(\frac{1}{x}\right)\right)

Using the product rule:

\frac{d}{dx}(uv) = u \frac{dv}{dx} + v \frac{du}{dx}

where $u = x$ and $v = \ln\left(\frac{1}{x}\right)$ , we calculate the derivatives:

\frac{du}{dx} = 1

and

\frac{dv}{dx} = \frac{d}{dx} \ln\left(\frac{1}{x}\right) = \frac{d}{dx} \left(-\ln(x)\right) = -\frac{1}{x}

Substituting these into the product rule:

\frac{dP}{dx} = x \left(-\frac{1}{x}\right) + \ln\left(\frac{1}{x}\right) \cdot 1 = -1 + \ln\left(\frac{1}{x}\right)

To find the maximum probability $P$ , we set the derivative equal to zero:

-1 + \ln\left(\frac{1}{x}\right) = 0

Thus, we have:

\ln\left(\frac{1}{x}\right) = 1

Exponentiating both sides, we get:

\frac{1}{x} = e

Therefore, $x = \frac{1}{e}$ , which means the probability is maximized when $\frac{r}{N} = \frac{1}{e}$ .

Maximum Probability

At this optimal point, the maximum probability is:

P = P_{max} = \frac{1}{e} \approx 0.368

This shows that the optimal strategy is to sample approximately $\frac{1}{e}$ (about 36.8%) of the total treasure boxes and then select the next box that is greater than all the ones in the sample. This strategy maximizes the chance of selecting the highest prize.

Program Simulation

We can use TypeScript to simulate the process described above.

To verify the probability of winning the highest prize using this strategy, we can calculate the ratio of successful trials where the highest prize is obtained to the total number of trials. Below is a TypeScript program that simulates this process:

function simulateGamblingGame(m: number, x: number, trials: number): number {
  let successCount = 0;

  for (let trial = 0; trial < trials; trial++) {
    const boxes = Array.from({ length: m }, () => Math.random() * x);
    const firstPart = boxes.slice(0, Math.floor(m * 0.37));

    // Remember the highest prize in the first 37% of boxes
    const p = Math.max(...firstPart);

    // Find the maximum prize in all boxes
    const maxPrize = Math.max(...boxes);

    // Check from the 37% onward if a prize higher than p is found
    for (const prize of boxes.slice(Math.floor(m * 0.37))) {
      if (prize > p) {
        if (prize === maxPrize) {
          successCount++;
        }
        break; // Stop once a higher prize is found
      }
    }
  }

  return successCount / trials; // Return the success probability
}

// Set parameters
const m = 100; // Total number of boxes
const x = 1000; // Maximum prize in each box
const trials = 100000; // Number of trials

const successProbability = simulateGamblingGame(m, x, trials);
console.log(`Probability of winning the highest prize: ${successProbability}`);

Explanation

Parameters:
- m: Total number of treasure boxes.
- x: Maximum prize in each box.
- trials: Number of simulation trials. More trials increase accuracy.
Simulation Process:
- Randomly generate the prize for each box.
- Calculate the maximum prize in the first 37% of the boxes (p).
- Find the highest prize (maxPrize) in all boxes.
- Starting from the 38% box, check if there is a prize higher than p and if it equals maxPrize.
Result:
- Return the probability of winning the highest prize after many trials.

Running this simulation produces a result like this:

Probability of winning the highest prize: 0.367999

As shown, the probability of winning the highest prize increases to around 37%, which is a significant improvement from 0.1%.

To further verify, let's simulate the probability of winning the top $t\%$ prizes by dividing the prize ranges into $10\%$ increments (e.g., top 10%, top 20%, etc.).

Modified TypeScript Code for Different Prize Ranges

function simulateGamblingGameWithRanges(
  m: number,
  x: number,
  trials: number
): number[] {
  const successCounts = Array(10).fill(0);
  // Array to store the number of successes in each range

  for (let trial = 0; trial < trials; trial++) {
    const boxes = Array.from({ length: m }, () => Math.random() * x);

    const k = Math.floor(m * 0.37);
    const firstPart = boxes.slice(0, k);

    const p = Math.max(...firstPart);

    let chosenPrize = 0;

    // Find the first box greater than p after the first 37% boxes
    for (const prize of boxes.slice(k)) {
      if (prize > p) {
        chosenPrize = prize;
        break;
      }
    }

    // If no box greater than p is found, select the last box
    if (chosenPrize === 0) {
      chosenPrize = boxes[boxes.length - 1];
    }

    const sortedBoxes = [...boxes].sort((a, b) => b - a);

    // Determine the prize range that the chosen prize falls into
    for (let i = 1; i <= 9; i++) {
      const thresholdPrize = sortedBoxes[Math.floor((m * i * 10) / 100)];
      if (chosenPrize >= thresholdPrize) {
        successCounts[i - 1]++;
      }
    }

    // The top 100% prize is always chosen, so increment this count
    successCounts[9]++;
  }

  // Convert counts to probabilities
  const successProbabilities = successCounts.map((count) => count / trials);

  return successProbabilities;
}

// Set parameters
const m = 100; // Number of boxes
const x = 1000; // Maximum prize
const trials = 100000; // Number of trials

const successProbabilities = simulateGamblingGameWithRanges(m, x, trials);

// Output the probabilities for each prize range
for (let i = 1; i <= 10; i++) {
  console.log(
    `Probability of winning a prize in the top ${i * 10}%: ${(
      successProbabilities[i - 1] * 100
    ).toFixed(2)}%`
  );
}

Results from the Program

Probability of winning a prize in the top 10%: 66.96%
Probability of winning a prize in the top 20%: 70.67%
Probability of winning a prize in the top 30%: 74.42%
Probability of winning a prize in the top 40%: 78.06%
Probability of winning a prize in the top 50%: 81.70%
Probability of winning a prize in the top 60%: 85.45%
Probability of winning a prize in the top 70%: 89.14%
Probability of winning a prize in the top 80%: 92.84%
Probability of winning a prize in the top 90%: 96.60%
Probability of winning a prize in the top 100%: 100.00%

We see that, using this strategy, we maximize the chances of getting a high-value prize.

Conclusion

The simulation verifies that selecting 37% of the boxes first and then choosing the next box with a prize greater than the maximum from the first 37% is the optimal strategy. This maximizes the probability of winning the highest prize, known as the 37% rule.

This strategy can also be applied in real-life scenarios, such as making optimal choices in uncertain situations.

NOTE & BLOG